For a long time Han and I are doing tests for various lock manufacturers. At the beginning, most of the requests were concerns if the ‘bump proof’ pins they came up with were really bump proof. And most of the time they were not.
On average it took three rounds of testing (and back to the drawing board) before we could not bump open the lock anymore. In some instances we supported the manufacturer with some technical advice to really make the lock bump proof (or highly bump-resistant).
And of course we have been thinking about designing our own bump-proof pin. We labeled it ‘the search for the golden pin’.
In our view, the golden pin has to have (at least) the following properties:
1) Prevent bumping one hundred percent (bump-proof, must withstand ‘advanced bumping’)
2) If possible, make other kind of attacks more difficult (like picking, impressioning and decoding)
3) The solution must contain not too many parts and must be easy to manufacture
4) Easy to Add to a classic 5 pin tumbler lock without modifying the core or house (too much)
5) If possible the ‘golden pin’ must be implementable in dimple and or other pin-tumbler style locks
6) Free of patents
Han and I have been partly successful in this search. And still we are having new ideas and brainstorm/try out sessions on a regular basis.
But ever since our trip to Vienna, our way of looking at the problem has changed.
We learned that if you ever want to have your invention implemented by a lock manufacturer, stop searching for a ‘golden pin’, and start searching for a ‘golden key’!
That is right, lock manufacturers are under constant pressure to come up with new patents on keys. A ‘patented key’ is required in all serious projects, and when a patent is ‘end of life’, so is the commercial success of the lock. Or actually a couple of years before the expiration of the patent (after all, who wants to buy something that will lose it’s ‘copy protection’ in three of four years?).
In a way it is a very healthy system. It keeps lock companies innovative. They can not just design a lock once and live of that design for ever. It forces them to keep investing in engineering.
The flip side it that great locking systems all of a sudden become ‘worthless’ because of the patent expiration. And in some instances that is not fair if you look at the level of security the lock and keys are still providing.
Looking at our mailbox, we are not the only ones looking for the golden pin….
A couple of times per month we receive mail from people who came up with pins or solutions against bumping. In almost all cases the six above properties are not met.
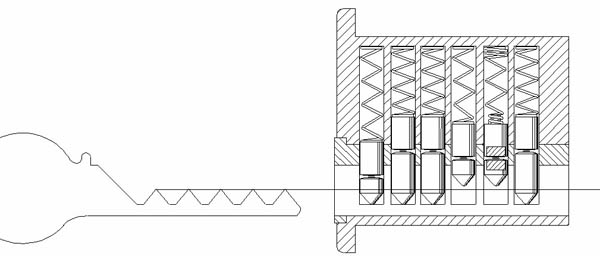
One of the last mails I recently received was from a gentleman called Ian Cecil from Australia. His invention is somewhat smart and makes use of the ‘floating pin’ principle. With that I mean that one of the pins is not reaching the ‘9’ position. We have first seen this solution in CES locks where they simply did not drill the hole in the plug all the way. And other floating pins can be found in systems like GeGe Pextra, Nemef and Master padlocks.
But before I take you to all the solutions we found in various locks, back to Ian:
Ian cam up with the following idea: Use a short spring that is connected to the ‘stopper plug’ and the ‘bottom pin’. And the bottom pin is by magnetic force attracting the top pin. If you keep the top pin small (0-3), the bump key can not make contact and obviously does not work. As I said, a nice invention but far from ‘bump proof’. The lock can still be opened by ‘advanced bumping’.
How does advanced bumping works? If I know there is a floating pin inside a lock, all that is required is a set of probe keys to determine the position and minimum depth of the floating pin. And once that info is decoded all I need to do is cut a 99949 key and open the lock.
Still, Ian makes a lot of sense on his website and shows he does know what he is talking about. Who knows, maybe he will come up with a ‘golden key’ one day ….

Idea that sort of came from GTV, would be hardened pins made of different materials, that have a specific gravity.
I have a different theory on Lock Bumping and Picking that may explain many pick/Bump proof pin ideas dont work
The usual way of explaining how bumping works is like 2 balls hit together.
1 stops 1 keeps going. Transference of energy.
If you look at bumping the pins do not separate in this way. The Spring
acts as a dampener and does not allow separation at all.
Separation of the pins at the shear line only happens because the chamber is not straight (due to turning pressure) and the bottom pin can not pass through a bent hole.
A better theory would be that “a straight pin (Bottom Pin) cannot pass through a bent hole.”
This explains why tapered ends on bottom pins do work to some degree to slow
down lock bumping.
Explains why magnetic pins dont stop bumping.
Explains why adding heavier springs dosent work.
Explains why light Top Pins dont stop Bumping/Picking.
Also explains why most ppl and manufacturers cant make bump/pick proof locks for inline cylinders.
It is just a theory, but it fits better to truly understand the principles.
To most ppl it dosent really matter. Like the earth is the center of the
universe….. 🙂
Ian Cecil
would a magnet not lose its strength after several bumps?
No.
There are different types of magnets. Rare Earth Magnets do not generally lose their magnetism. BTW only a small magnetic force is needed to make the magnets stick. The magnet is not designed to hold the pins together to stop bumping. Only to hold it away from the bottom of the chamber.
Ian
“If you look at bumping the pins do not separate in this way. The Spring
acts as a dampener and does not allow separation at all.”
Yes it allows separation, if you hit hard enough, the energy transferred to that top pin will bounce and in the process compresses the spring. The lower pin still sits still, so there is a gap.
Remembe, there is no turning pressure when you hit the key: You turn the bump key AFTER you have hit it.
Ian: Your ‘bent hole’ theory is partially right. Once a top pin is fired out of the chamber, it can no longer enter the core when there is the slightest degree of rotation. That is why pins with a narrow end can still fall back into the core and prevent it from turning. They can still fall back even if the core is rotated a couple degrees. Pins with a narrow tip require a much better timing and in some cases make it impossible to bump.
But as far as I see, the bumping energy is released to pins that are bound, even if they are slightly bound. The pins will fly like the cork of a bottle of champagne because the energy can not travel trough the metal when it is under pressure. Instead of traveling trough the metal, the energy will be used to ‘free’ the bound pin. This is one of the reasons why adding an extra element above the top pin (and sheerline) does not work (well). If the top pins are under pressure, all parts above that will be forced up.
The Oz suspended pin is protected by a US and UK patent application files about 18 months ago.
There are actually only a few UK Master Locksmiths who are fully aware of the actual underlying physics behind ‘bumping’. Just about everything I’ve seen written by so called experts is wrong but I aint going to point them in the right direction.
There are several interesting theories about how bumping works, incl. one by Master Lock found e.g. at http://www.thelockman.com/ – based on high speed video images of a bumped lock (either transparent or cutaway, I guess).
Anyway I believe there are different things that can happen depending on the weight of the pins, the properties of the springs, the technique used, etc. The momentum transfer is definitely one of them.
Bent holes would be an interesting explanation, too, but it seems to me that neither pin would move properly in such a bent hole. Maybe the torque is not so high in that application either.
Cheers,
mh
It would be interesting if lock makers some how threaded the inside of the pin chambers and took out the springs so they would rely on gravity. The pins would catch in the cylinder but not sure if it would cause too much wear on the pins and or the cylinder or if they would jam up and the lock would break
Every theory even so called facts have to be challenged.
So here is an experiment everyone can do.
1. Make a cutaway cylinder so you can see the top pins.
2. When you hit the Bump Key, what would you expect to see? The current theory would suggest you would see the top pins fly up above the shear line, just for a millisecond. Also you would see the top pin with a large bottom pin fly up further?
3. So keeping the cylinder perfectly lined up bump away…
4. Anyone with a high speed camera should be able to photograph the pins separated. (personally i have not seen this). They only separate when slight turning pressure is applied no matter how hard you hit it.
I would also suggest that the practice of turning the bump key just at the right time is also not correct. It is better to have a constant pressure like picking.
No pressure at all dose not cause any separation of the pins. so no point trying to get the timing correct.
Ian
Ian, could you please tell me where all the bumps energy then goes, if the top pins don\’t jump?
Yep, i think the bump energy is dampened by the springs?
Ian: I have my doubts, but will give it a try this evening…. (and let you all know)
Ian, what you suggest sounds like an overlifting attack. It doesn’t seem to depend on the speed of the pins, just use a tool to lift all the pins up, then let them fall down while tensioning, the effect should be the same?
Cheers,
mh
Ian, if the energy is dampened by the springs, it means that the springs must compress and this means that something compresses them and that something is the top pins.
Ian: I did some experiments, and found the pins move so quickly you can not see it. But they do move, even when the key is not under pressure. Will blog about it someday soon.
If you hit the bumpkey with the speed of 1m/s then you have a widh of approx. 5 milisecond to turn the key, hence it is useless to try to turn AFTER you have hit the key. Human reaction time is not that fast. So there is something in Ian,s theory. Had been very nice to see that highspeed camera movie, unfortunately was it restricted.
However, point two… Impressioning protection is easy to obtain if you use same kind of lower pin as in Assa 700 SCD locks. When you are near the cheer line, turning the plug will rise the pin and make it impossible to make marks on your blank. That is one of the things that Han didn’t mention in the e-paper where this lock was described.
One more thing. I’ve never seen anyone bumping the Assa 700 SCD lock. Althought there is people who claims to have done that.
Thanks for humoring me 🙂
I admit i am wrong in saying that the pins never separate. Of course they do you can see this by the squashed springs.
But i dont think they have to seperate to open the lock??
I think i can prove what i am saying.??
take a look at the master bump stop video
http://www.youtube.com/watch?v=QiddbiV0MdI
I think they got it completely wrong :)))
Here is a quick sketch of what i think is happening
http://24hourlocksmith.com.au/news.htm
How to prove it?
Well if you have a cutaway cylinder you can see it!
If you havent then you can feel it. Insert a key into a lock with slight turning pressure. It will go in a bit then bind(depending on the high/low cuts of your key).
When the key is inserted with slight turning pressure look at what happens.
The Top Pins push up out of the road very easily. But when the key has a high spot that pushes a bottom pin above the shear line the key (and bottom pin) gets stuck.
You can see with a cut away cylinder that the bottom pin cannot enter the top of the cylinder because the pin chamber is bent.
I will take a photo to show you when i find my camera. It is plain as dogs balls.
Ian
1 more thing..
So who cares?
well if you are a manufacturer like master or Ilco( with their Bump Halt) You would look pretty silly if you didnt understand how Bumping worked and made a product based on the wrong principles that didnt work….
Ian
Barry switching from “golden pin” to “golden key” is the wrong approach. Making the key the focal point takes the most important person the locksmith completely out of the equation. This is the direction most lock manufacturers are moving. We are working on a cylinder with “golden pins plus traps” this approach makes it easy for the locksmith the solve the customers problem fast and easy. No delay in cutting the key. In fact the standard key is used. How do the locksmith feel about this?
As I understand it the pins actually get bashed around and apart quite a bit. Testing done on cutaways showed that the force was still present enough even in the keypin that when the lock opened the keypin (no longer restricted by the housing as it was a cutaway) flew out of the plug completely. There is a LOT of force going into those tiny bits of metal. It really knocks them around more than a single separation.
Mmmm, I’m not being as eloquent as I usually am, but this has to be a quick note, unfortunately. Anyway – Master wasn’t wrong, but at higher speeds it’s revealed that the pins are really ricocheting off of each other 3 or 4 times, not just one quick separation. Anyway – as mh said, all of this is likely dependent on a host of variables, so getting controlled, confirmable testing is going to remain a difficult task.
Ian, I like your picture, it’s like picking all pins at the same time, with the key pins stopping at the shear line. That would not work with a spool driver pin, though, as that type of pin would not move past the ‘bent hole’ either. So I guess there must be other effects happening, too.
@ mh
The spool top pin is interesting. I thought also as you said that it would get stuck. But look at it in a cut away cylinder, it acts same as other top pins.
@ Schuyler
The force is much greater with a Pick Gun then with Bumping.
Why does a bump key work better on a good quality lock(tight tolerances)then a Gun? (generally)
Maybe because the gun has too much force, as you said it bounces the pins too much and forces the bottom pins past the shear line and the bump key is more controlled? Maybe?
@ Bob
I agree with Barry, The Key is where the $ is.
Adding bump proof pins can be more beneficial to the locksmith though.
Up selling with Bump Proof pins makes good sense, especially when you combine it with a registered design key system.
Makes other registered design key systems obsolete… (see why other locksmiths hate me)
Ian
> The spool top pin is interesting. I thought also as you said that it
> would get stuck. But look at it in a cut away cylinder, it acts same as
> other top pins.
This could mean you might want to refine your theory, so that it can explain this effect as well?
Ian, I don’t believe your bent-hole theory of bumping adequately explains the phenomenon. Whilst I agree with what Barry said – it is entirely possible that your theory does contribute to successfully bumping a lock in some instances, I believe it is only a minor factor.
Consider the common bumping technique before the minimal-movement method was popularised – the 999 key was inserted, pulled back one space & then struck.
In any lock with at least one long key pin, when bumped by this method, each long key pin will be forced up above the shear line as the peak of the key passes underneath it.
Yet locks with long pins are bumpable using the pull-out method.
I suggest that when the key is struck, both the top pin and key pin are forced violently upwards, and they most likely don’t separate on the way up, as you have pointed out.
However, I believe separation of pins DOES occur.
It occurs as the pins are moving downards. This can be a bit hard to visualise, the easiest way I can explain it is that there is a time where the key pin has started to decend, but the top pin is still pushing up against the spring – hence a gap is between the pins… when this gap is at the shear line, thats obviously the window-of-opportunity in which to turn the plug.
Here is an interesting experiment that I believe proves my point – assemble a cylinder with a few really short key pins in it. Now bump this lock a few times, using the minimal movement method.
Each time you bump the lock, keep the plug turned & remove it from the shell.
I guarantee you (I’ve experimented with this), that some of the time you will find both the very short key pin and the top pin in the housing(shell). This fits in with the mechanism for bumping that I described above – the pins were forced, together past the sheer line. The very short pins were still in the shell at the time the other key pins were in the plug, with a small gap between them and their top pins. This happens when using the minimal movement method, as well as when using the older method.
I think comparing bump keys to pick guns is misleading & leads to misunderstanding. I believe that with a pick gun, there is a separation of pins caused on the ‘up’ stroke. The pick gun used correctly ‘taps’ the bottom pin momentarily. I feel that the bump key (even with minimal movement technique) is pushing upwards on the key for more time (albeit fractions of a second), resulting in key pin and top pin being violently pushed up together.
I hope I’ve explained my thoughs clearly.
…mercurial
mercurial,
The concept you described is shown as a computer graphic animation in the Master Lock Bump Stop video:
http://www.youtube.com/watch?v=Ip_z2-iiKvQ
The problem I have with that theory is this:
There can be only two reasons why the pins separate on the way ‘down’:
1) gravity
2) elastic collision
Because the theory says the pins do not separate on the way ‘up’, 2) is not an option, so it must be gravity.
But then the easiest way to prevent bumping is to mount the lock upside-down. However, we already do that in many parts of Europe, yet bumping also works here. And last time I checked, the gravity was not upside-down here 🙂
So this theory is somewhat non-complete…
BTW, the Bump Stop pin itself does of course work to stop “non-advanced” bumping, as Barry has put it. It’s just the explanation I don’t buy…
Cheers,
mh
I continue to posit that the pins are being BASHED around like crazy by the force. There isn’t a single separation in either direction, they separate and rejoin multiple times.
quoting myself
> There can be only two reasons why the pins separate on the way ‘down’:
> 1) gravity
> 2) elastic collision
I think I missed a part of 2) – indeed there can be a more or less elastic collision when the pins hit the end of the hole.
Now the scenario shown in the high speed photography Master Lock commissioned (which I unfortunately never saw myself)
– which says that the pins separate for the first time on the way back –
makes sense to me;
I also concur with Schuyler that they will probably bounce back and forth multiple times, but the first window when they all separate at a similar time seems to be the best opportunity to turn the plug.
Cheers,
mh
Agreed with mh’s final statement there.
It is interesting to read the various theories, none of which are actually based around good science. There is no mystery as to how locks can be bumped but only a handful of people know what it is.
High speed video does NOT disclose the science and has led many up the wrong garden path.
Given the exposure and interest bumping caused over the last couple of years, it is quite amazing that so much ignorance still abounds. Within the various postings there are elements that are correct but none are strung together to form an accurate account.
Our detailed research into bumping was concluded over a year ago. We filed a total of 7 patents but only 2 will survive due to prior art.
John
John: If you have the answers, where do we find them? Is your research published anywhere?
Hi Barry,
Our research has been disclosed to various parties in confidence, including a few lock manufacturers and UK master locksmiths in closed session. This was more of a demonstration of what actually occurs but without going into reams of maths/physics. To demonstrate we showed the worlds first computer software that actually calculates with great accuracy what occurs and there are dozens of variables to play with.
The maths is so complex that even a fast computer takes about 20 seconds to plot the reaction of all the components after the key is struck.
I am very lucky in that my partner is a world expert in his field and a pioneer of dot matrix print heads. He applied his mind to the physics of bumping when it blew up. It was a real eye opener and taught me a great deal. Perhaps the most important thing I learnt was not to assume anything. Everything to do with physics can be expressed mathematically. You dont need to see anything. You can calculate with great accuracy how any object will react. Using ones imagination does not work; what is going on is far too complicated to visualise without having real data to interpret.
Our software can reverse engineer ‘solutions’ and test effectiveness, which is the main reason we compiled it.
We spent about 6 intensive months examining the physics and to date we havent made a penny, however knowledge is profit in itself. We got right up the nose of some so called engineers; they were very intimidated indeed. There has never been a need for locksmiths or lock manufacturers to have expertise in higher mechanics and maths. I dont have it either but Im real pleased my partner has !
John
John: Well … thanks for clarifying 😉
What would it take to show me what you showed the other parties? 😉
I dont have a problem as such showing what happens because that doesnt really disclose the why. What the software does is allow the user to vary a comprehensive set of variables. These include basic cylinder geometry, mass of upper and lower pins, pin length and material, bump key dimensions and materials, input force, spring pre-load and spring rate, magnetic coupling, damping and several others. The results are displayed as lines on a graph, accurate to 3 decimal places. There are no graphics or animation, just fundamentals. The software is DOS based and is basically a collection of extremely complicated mathematical formulae.
The results are NOT predictive or intuitive. Newtons Cradle has very little to do with bumping. Skill also has very little to do with it, especially timing when torque is applied.
I can state a few facts: The force applied during bumping is overwhelming. The bump key tips do NOT need to go anywhere the lower pins. Tollerances have a great impact, ESPECIALLY front to back play between the plug and shell.
I can state what does not work: Changing spring rates, adding or removing pin mass, adding dampers including grease and the rubbish called Pick Buster.
There are things that can be done that will increase resistance only and if you understand exactly what is going on these can be defeated quite easily.
A very good analogy is throwing 5 poker dice. if you are real lucky you will get 5 aces first time. If you get say two ( and you dont know if you have) then thowing the remaining dice might result in another Ace and so on until the lock is bumped. However you also dont know where any of the pins actually are at any one time between bumps. It could be that you have a combination of drivers and differs blocking the shearline. Since you cannot tell you cannot use skill to affect the almost totally random nature of the results of impact.
No matter how a pin tumbler lock is designed there will always be at least one pin set left blocking the shearline if you dont get 5 aces first impact. The counter measures put in place to increase resistance will tend to become ‘last man standing’ ( assuming the measure has some merit). When you get to that stage you can apply skill based on knowledge to get around the measure. In a way some measures actually help bumping because they are the last man standing. If they were not present you wouldnt have a clue what you were up against and chance/odds would come into play again.
John
– I forgot to mention that gravity is irrelevant but what the cylinder is mounted in is IE holding in your hand is NOT the same as being mounted in a lock case.
John
John, it’s interesting to hear that you applied scientific methods to this, sad to hear you didn’t make a penny.
Now, with a simulation, you use a model of the real world, i.e. you make simplifications; with your friend’s experience you have most probably made the right decisions on this; still – how did you verify your assumptions on friction and the statistical variations of the ‘bump’ itself? Did you do measurements on real locks to compare results, and how did you make sure the measurement itself didn’t change the result? Like cutaway locks may behave different from closed locks?
Also, what do you mean with “The bump key tips do NOT need to go anywhere the lower pins”?
Cheers,
mh
Also, a DOS program? Doesn’t sound credible, because usually these tasks and the people who are versed in physichs use MathLab and it is quite a standard.
John, you are saying much but nothing yet, so could we have either images or some explanation of what really happens when bumping? Because you haven’t told anything new yet and haven’t trashed Newtons cradle -theory in any way.
Don’t take this harshly or anything, I’m just pointing out facts.
John you have a flaw in what you are saying above.
About throwing maybe 5 aces?? and not knowing where the pins are between bumps.
That dosent explaing why some locks bump first time every time… Ok you really didnt explain anything.
But the “bent hole theroy” explains why you can bump a lock first time every time (Sometimes) no aces just simple observation.
When turning pressure is applied the top pin moves easily, but the bottom pin cant pass the shear line.(easily)
Ian
Sorry i didnt explain it very well, but what i mean is that it is not random as you are saying.
Ian
Mh i would like to see masters’ high speed pics of bumping. How is it possible that the pins can separate on the way back down, under spring tension? Shouldn’t the spring compress the top pin and force it onto the bottom pin under pressure. The bottom pin cant magically accelerate on its own, especially with the top pin accelerating under spring tension.
Ian
Ian, the pins can separate on the way fown, but more specificly the top pin is either moving up or staying in place, while the bottom pin starts to ascend.
Plain physics: When the bumpkey hits the pin pair, the top one gets all the energy and jumps, but at the same time the bumpkeys little “notch/triangle/slope” lifts the bottom pin a little and it will jump because of that, but it has far more less energy than the top pin, so it starts ascending much before the top pin. The top pin is cushioned by the spring, stopped and then it comes back down.
Your “bent hole” -theory doesn’t explain spools and other security pin systems bumping the first time, so there is a flaw.
ok i will try to get proof 🙂
Jaakko, why should the top pin get ALL the energy?
An interesting article on the topic of momentum and energy transfer can be found here:
http://www.lhup.edu/~dsimanek/scenario/cradle.htm
(esp. #14, as not all pins have the same size, and the bumpkey is also not just another pin of the same size that’s fired at the key pin…)
Cheers,
mh
Ian –
from LP101:
“i would postulate that the pins separate on the BOTTOM pin’s way down, but the top pin is still traveling up.
consider:
the newton’s cradle analogy is still accurate, but due to surface adhesion and an imperfect collision, both pins move upward. the top pin is given more energy than the bottom pin, but due to the spring effect slowing it, and the possible adhesion of the bottom pin, both move upward.
at some point, the fact that the lower pin has less energy causes it to slow, but the higher energy of the top pin allows it to continue. the bottom pin slows, stops, and starts to fall, but the top pin is still traveling upward, as it has a higher apogee.
by the time the bottom pin falls past the shear line, the top pin has reached it’s peak, and started falling, however since it’s peak was higher, there’s a gap. bump successful. at this instant, both pins may be traveling down, but they did not separate while both were traveling down.”
mh, sorry about that 🙂 I thought I would rewrite it in other words, but thought that whatever, it basicaly gets all the energy, atleast when cmpared to the bottom pins energy content.
Barry,
E-mail me and I’ll start to detail what actually occurs and why.
John
Jaakko,
E = 1/2 m v^2
I think it’s entirely possible that the slope of the key forces both pins to move at the same speed.
Cheers,
mh
I cannot wait to see you all again at the open 🙂
hehehe, me toooooo 🙂
mh, possible, but the upper pin should get more energy (thus speed) than the bottom, because if they travel the same speed, they will not separate 🙂 But as you said, possible situation.
Schuyler, mh, Barry, whoelseiscoming, we’ll see there if you guys buy my tools 😉
One thing to note about the Newton’s Cradle analogy is that by the mathematics of elastic collisions, perfect momentum transfer from the lower to the upper pin only happens when the two pins have equal mass. If this is not so, then the lower pin continues in motion. In particular, if the top pin is lighter, the lower pin continues up with it (but at a lower speed than it), while if the top pin is heavier, the bottom pin rebounds back towards the bottom of the lock (where it immediately hits the bump key again). The bottom pin is only left motionless if its weight is equal to the weight of the top pin. In the Newton’s Cradle, all the balls have the same weight, making for near-perfect momentum transfer; but in locks, top and bottom pins have different weights.
The math of elastic collisions isn’t a perfect way to model a lock, but it’s a good first step.
In trying to prove my bent hole theory i may have overlooked the obvious. (sort of):(
Here’s why.
When i was looking at the pins when bumping there was no separation as in Newtons cradle(that i could see). It looked like the bottom pins were just bouncing the top pins up and the bottom pin couldn’t go past the shear line.
But actually i think i got it upside down.
what is happening is that
when turning pressure is applied to the barrel
1. The top pins bind.
2. The bottom pins bump the top pins above the shear line
3. The top pins want to fall back down but cant enter the barrel because the cant fit.
The Top Pins cant possibly fall back down because the barrel has turned just a fraction more from where it was when it was binding. So there is no round hole to fall back into.
The Newtons cradle theory is great but has flaws. Put a spring on the end of the last ball and see what happens. All the balls stop dead. Because the top pin binds in the lock the spring has no effect.
The important bit is that when you are bumping a lock the top pin and bottom pin don’t have to separate as in a newtons cradle. The top pin just has to be pushed above the shear line. In fact i would say the bottom pin acts more like a hammer. It has to overcome the friction of the binding top pin & push it above the shear line.
Spool pins work same way, no difference. (unless it is the last one to be pushed up??)
Locks with tighter tolerances and better machining are likely to have the top pins bind at the same time? Hence only 1 hit is necessary. The only randomness is caused weather the top pins all bind at the same time or not.
I made a large pin chamber, top pin and bottom pin to test the theory and see what was happening. I will take a video and post it when i can.
Ian
Has anyone tried adjusting the top pin size to complement the bottom pin size? That is say if a Kwikset had a bitting of 2 5 3 6 4, then use pin numbers 6 3 5 standard-top-pin, and 4 for the top pins (perhaps filing down the bumps to a flat surface on those larger top pins and perhaps cutting slots for them to false set as if they were spool or serrated. The differing masses and spring compression should confound the lock bumping a fair bit. If the working mechanism is purely the top pins binding and not reentering the plug cause they basically set as the plug is under tension then the false sets from security pins should help unless the energy is so sudden as to skip over the false sets. I’d like to see an experiment to see if spool and mushroom pins would false set during lock bumping.